运算定律
一、【教学内容】
运算定律
二、【教材分析】
1、有关运算定律的知识相对集中,有利于学生形成比较完整的认知结构。
2、从现实的问题情境中抽象概括出运算定律,便于学生理解和应用。
3、重视简便计算在现实生活中的灵活应用,有利于提高学生解决实际问题的能力。
三、【教学目标】
1、引导学生探索和理解加法交换律、结合律,乘法交换律、结合律和分配律,能运用运算定律进行一些简便运算。
2、培养学生根据具体情况,选择算法的意识与能力,发展思维的灵活性。
3、感受数学与现实生活的联系,能用所学知识解决简单的实际问题。
四、【教学重、难点】
重点:探索和理解加法交换律、结合律,乘法交换律、结合律和分配律,能运用运算定律进行一些简便运算。
难点:探索和理解加法的乘法的运算定律,会应用它们进行一些简便运算。
五、【教学策略】
1、充分利用学生已有的感性认识,促进学习的迁移。
2、加强数学与现实世界的联系,促进知识的理解与应用。
3、注意体现算法多样化、个性化的数学课程改革精神,培养学生灵活、合理选择算法的能力。
教学课题
加法交换律和结合律
教学目标
1、知识与技能:①结合具体的情境,引导学生认识和理解加法交换律和结合律的含义。
2、过程与方法:能用字母式子表示加法交换律和结合律,初步学会应用加法交换律和结合律进行一些简便运算。
3、情感态度与价值观:①体验自主探索、合作交流,感受成功的愉悦,树立学习数学的自信心,发展对数学的积极情感。②培养学生观察,比较,抽象,概括的初步思维能力。
教学重点与难点
1.重点:认识和理解加法交换律和结合律的含义。
2.难点:引导学生抽象概括加法交换律和加法结合律。
教学准备及手段
多媒体课件
课型
新授课
教学流程
1.引入谈话。
在我们班里,有多少同学会骑车?你最远骑到什么地方?
骑车是一项有益健康的运动,这不,这里有一位李叔叔正在骑车旅行呢! (多媒体演示:李叔叔骑车旅行的场景。)
2.获得信息。
问:从中你可以得到哪些信息? (学生同桌交流,然后全班汇报。)
问题是什么?
3.解决问题。
问:能列式计算解决这个问题吗? (学生自己列式并口答。)
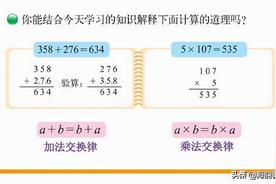
1.加法交换律。
(1)解决例1的问题。 根据学生回答板书:
40+56=96(千米) 56+40=96(千米)
问:两个算式都表示什么?得数怎样?○里填什么符号?
40+56○56+40,
(2)你能照样子再举几个例子吗?
(3)从这些例子可以得出什么规律?请用最简洁的话概括出来。
(4)反馈交流。 两个加数交换位置,和不变。
(5)揭示定律。
问:①知道这条规律叫什么吗?
②把加数换成其他任意的数,交换律还成立吗?
③怎样表示任意两数相加,交换加数位置和不变呢?请你用自己喜欢的方式来表示,好吗?(同桌轻声交流)
④交流反馈,然后看书:看看课本上的小朋友是怎么说的。
⑤根据加法交换律对口令。
师:25+65=______ 78+64=______
⑥完成课本第18页下面的“做一做”1
2.加法结合律。
多媒体展示:李叔叔三天骑车的路程统计。
(1)找出信息解决问题。 问:你能解决李叔叔提出的问题吗? 学生独立完成后交流。
多媒体展示线段图:根据学生列出的不同算式,表示三天路程的线段先后出现。
问:通过线段图的演示,你们发现什么?(不论哪两天的路程先相加,总长度不变。)
我们来研究把三天所行路程依次连加的算式,可以怎样计算:
比较88+104+96 88+104+96
=192+96 =88+200
=288 =288
为什么要先算104+96呢?(后两个加数先相加,正好能凑成整百数。)
出示(88+104)+96○88+(104+96),怎么填?
(2)你能再举几个这样的例子吗?
问:观察、比较这些算式,说一说你发现了什么秘密?(鼓励学生用自己的话来说。)
(3)揭示规律。
三个数相加,先把前两个数相加,或者先把后两个数相加,和不变,这就是加法结合律。
用符号表示。(学生独立完成,集体核对。)
(▲+★)+●=____+(____+____)
(a+b)+c=____+(____+____)
(4)问:①用语言表达与用字母表示,哪一种更一目了然?
②这里的a、b、c可以表示哪些数?
(5)完成P18做一做2
1.指出下面哪几道题运用了加法运算定律,分别运用了什么运算定律。
(1) 验算:(运用了加法交换律)
(2)用“凑十法”7+9=6+(1+9)(运用了加法结合律)
(3)教材练习五
1.今天我们发现了哪些数学规律? 2.这些运算定律是怎样发现、归纳的?
3.对于加法的交换律、结合律的应用,我们已经知道的有哪些?